A new Adaptive Quantization based on a color dependent noise sensitivity
measure
H. Galleron
20 May 1998
Abstract
In this paper, several adaptive quantization algorithms are tested and
compared: The Activity Model of TM5, a new color dependent model and combinations
of both of them. The color dependent method is based on a Perceptual Noise
Sensitivity Measurement. Applied alone to a video, this method doesn't
improve the picture quality at a constant bitrate. Combined with the Activity
model, it brings however some improvements, but unfortunately relatively
small. In the last section, some other possible Adaptive Quantization methods
are discussed.
1 Introduction
By now, the TM5 implementation of the MPEG-2 standard gives very good
results but is still not optimized, especially concerning the quantization
part of the algorithm. It uses indeed an adaptive quantization, but only
depending on the activity of luminance blocks. In this paper, a new adaptive
factor is introduced, based on the perceptual noise sensibility of colors.
Unfortunately, by now, the model described in section is not improving
the picture quality consequently. But further modifications are still possible,
they are discussed in the last section of this paper.
2 Description of the compression
algorithm
2.1 Presentation of the
Algorithm
The different adaptive quantization algorithms are not tested directly
with TM5, but with a more simple compression algorithm using only I-frame.
It is described in the Figure .
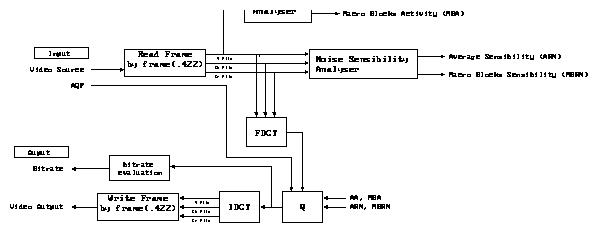
Figure 1: Algorithm of a simplified I picture encoder/decoder
The different parts are basically the same than the equivalent ones
in TM5, except for the rate control and the calculation of the Quantization
factor. In TM5, an Average Quantization Factor (AQF) is first calculated
depending on the video complexity and the target bitrate. An adaptive quantization
is then obtained by multiplying the AQF by a correction factor base on
the luminance block activity. The detail of the calculation is described
in Section .
In the case of the I picture algorithm presented here, the AQF is not
calculated within the program but is given in the input. The bitrate is
indeed supposed to be proportional to the entropy of the coded video. To
insure a constant bitrate, an independent module calculates retrospectively
the entropy of each frame just coded. The AQF can be then manually re-adjust
to make the calculated entropy fit with a reference one. The reference
entropy is chosen as the one of the same video input, without adaptive
quantization.
2.2 Evaluation of the bitrate
As explained in the previous part, the bitrate is supposedly proportional
to the entropy. In this part, the method for calculating this entropy is
reviewed. By scanning every blocks of a given picture, the density of probabilities
p(i) of each possible value i for the quantized DC and AC coefficients
is evaluated. The entropy is then obtained with the following equation:
| Entropy = |
2047
å
i = -2047 |
-p(i)logp(i). |
|
(1) |
2.3 Video files tested
in this report
Several video files are used in this paper: mobile1.422, popple1.422, flower1.422,
bicycle1.422, tennis1.422, confetti1.422 and hockey1.422. They have been
chosen because rich in terms of complexity and spatial and temporal activities.
The video format will always be .422 and no other format will be tested.
2.4 Method used for evaluation
To appreciate the picture quality of a video file, the following undesirable
effects are observed on a display: the flickering of the image, the Block
effect and the stability of chrominance bounds. Basically, an adaptive
quantization improves some parts of the pictures by coding more coarsely
some other regions. The final result is then obtained by comparing the
gain and loss in picture quality.
3 Adaptive Quantization method
3.1 Quantization principles
The Quantization algorithm applied to test the new adaptive quantization
method is the same than for TM5:
-
DC Coefficients
-
The intra_dc_precision (cf. MPEG-2 flow charts) is set to 10 bits. Therefore
the quantized DC value, QDC, is calculated as:
-
AC Coefficients
-
The AC coefficients ac(i,j) are first quantized individually:
| ac_quant(i,j) = |
32ac(i,j)
wI(i,j) |
, |
|
(3) |
where wI(i,j) is the (i,j)th element of the Intra quantizer matrix used
by default in TM5. All the ac_quant(i,j) are then quantized by the same
quantization factor AQ:
| ac_quant(i,j) = |
0.75AQ+ac(i,j)
2AQ |
. |
|
(4) |
AQ is obtained by multiplying AQF, given in input, by a correction factor
calculated for each macroblock. The final value for the quantized AC coefficients,
QAC is then given by clipping ac_quant(i,j) to the range [-2047 .. 2047].
In the following section, several methods for calculating this correction
factor are described. AQ will be calculated with one of the following equations:
where N-actj is the correction factor calculated with the activity model
and N-RN the one calculated with the noise sensibility model.
3.2 The Activity Model
3.2.1 Idea of the model
The model is based on the idea that the human eye is more sensible to imperfections
in a flat region than in a complex region. By allowing a bigger quantization
scale factor (AQ) for high detailed regions, the model reduces the entropy
and improves the picture quality.
3.2.2 Calculation of
the activity factor
The spatial activity measure for a macroblock j is calculated from the
four luminance sub-blocks:
| actj = 1+ |
min
n = 1,2,3,4 |
(vblkn), |
|
(8) |
where
| vblkn = |
1
64 |
|
64
å
k = 1 |
(Pkn -P_meann)2 |
|
(9) |
and
| P_meann = |
1
64 |
|
64
å
k = 1 |
Pkn. |
|
(10) |
Pkn are the original values of the luminance for
the n-th 8×8 block of the macroblock. The activity actj
is then normalized to N\actj with:
| N_actj = |
2actjj+avg_act
actjj+2avg_act |
, |
|
(11) |
where avg_act is the average activity for the frame to be coded. The final
value for the normalized macroblock activity N_actj is then
shifted so that its average value in the coded frame is 1.
3.3 The Noise Sensibility
Model (NSM)
3.3.1 Idea of the model
The study presented in ``Color Dependency of Perceptual Noise Sensitivity''
[] showed that the human eye response to a noise highly depends on the
color to which the noise is added. To apply this law to a compression algorithm,
the hypothesis is made that the flickering and Block effect perception
has the same dependence with the color.
In the NSM, the level of noise sensibility is first calculated for each
macroblock, function of its average color coordinates. Its normalized value
is then used as the correction factor N_RN.
This method takes into account the properties of the human eye and therefore
should improve the picture quality for a given AQF. But, contrary to the
activity model, it has the disadvantage of increasing the entropy. In other
words, the quality is globally decreased for a given bitrate, but better
dispatched. The model is therefore valid only if the gain in picture quality
compensates the necessary increase of AQF to maintain a constant bitrate.
3.3.2 Measure of the
Perceptual Noise Sensibility of a color
The Measure of Perceptual Noise Sensibility will be noted RNs
(Y,Cb,Cr). It is obtained by the following equation:
|
1
RNs (Y,Cb,Cr) |
2
|
= |
1
RNY,15 (Y,Cb,Cr) |
2
|
+ |
1
RNCb,15 (Y,Cb,Cr) |
2
|
+ |
1
RNCr,15 (Y,Cb,Cr) |
2
|
, |
|
(12) |
where RNY,Cb,Cr,15 (Y,Cb,Cr) are calculated with the tables
given in []. In this application, the value of aCb
and aCr are set respectively to 2
and 1 instead of 2.3 and 1.3, to increase the dependence on chrominance
coordinates.
3.3.3 Calculation of
the NSM correction factor
Each macroblock j is first divided in 4 subblocks. For each of them, the
average value of Y,Cb and Cr is then calculated. From this value, RNY,15,
RNCb,15 and RNCr,15 are calculated with the equations
(23), (24) and (25) of []. The above equation (12)
gives then RNs. In order to limit the decrease in picture quality,
the minimum of the four values is taken as the RNs,j of the
macroblock j.
RNs,j is then normalized with:
| N_RNj = 1 + amp× |
RNs,j
avg_RN |
, |
|
(13) |
where:
-
N_RNj is the final NSM correction factor for the MB j.
-
amp allows a control on the variance of the correction factor. Its value
are usually taken equal to 1,2 or 3. The model is then renamed respectively
NSM-1, NSM-2 and NSM-3.
-
RNs,j is the Measure of Perceptual Noise Sensibility of the
macroblock j.
-
avg_RN is the average value of RNs,j for the present frame.
The Figure illustrates the different steps in the calculation of the NSM
correction factor.
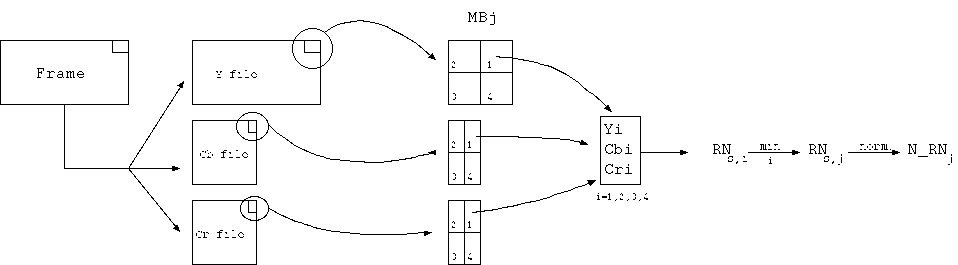Figure 2: Steps for the calculation of N_RNj
4 Performance of different
models for an Adaptive Quantization
4.1 Description of the
tests
Each of the video files described in section are processed with the I picture
encoder/decoder using the following Adaptive Quantization methods:
-
without Adaptive Quantization
-
with the Activity Model
-
with NSM-1
-
with NSM-2
-
with NSM-3
-
with a combination of the Activity and NSM-1
-
with a combination of the Activity and NSM-3
In each case, the variation of entropy is first calculated for AQF = 25.
For the different video, the AQF is corrected so that the entropy remains
constant for all methods. The value for the entropy is chosen equal to
the one obtained without Adaptive Quantization. Finally, an observation
on a display of the video processed with this new AQF is done to estimate
the improvement in picture quality. All these observations are described
in the next section.
4.2 Results
|
|
mobile |
popple |
bicycle |
cheer |
confetti |
flower |
hockey |
tennis |
|
| without Adaptive Q. |
0.64 |
0.42 |
0.46 |
0.54 |
0.44 |
0.55 |
0.29 |
0.40 |
|
| Activity Model |
0.64 |
0.38 |
0.45 |
0.53 |
0.43 |
0.52 |
0.28 |
0.39 |
| Activity / Without(%) |
-0.3 |
-9.9 |
-2.2 |
-0.7 |
-1.6 |
-6.3 |
-3.8 |
-2.5 |
| Equivalent AQF |
25 |
20 |
24 |
25 |
24 |
22 |
23 |
24 |
|
| NSM-1 |
0.68 |
0.44 |
0.48 |
0.55 |
0.45 |
0.59 |
0.29 |
0.43 |
| NSM-1 / Without (%) |
6.1 |
5 |
4.4 |
2.8 |
3 |
5.8 |
1 |
6 |
| Equivalent AQF |
27 |
28 |
27 |
26 |
26 |
27 |
28 |
26 |
|
| NSM-2 |
0.71 |
0.46 |
0.49 |
0.56 |
0.46 |
0.61 |
0.30 |
0.43 |
| NSM-2 / Without (%) |
11.5 |
10.1 |
6.8 |
4.3 |
5 |
10.5 |
2.8 |
6.7 |
| Equivalent AQF |
30 |
31 |
28 |
27 |
27 |
30 |
30 |
27 |
|
| NSM-3 |
0.76 |
0.49 |
0.50 |
0.57 |
0.47 |
0.65 |
0.30 |
0.44 |
| NSM-3 / Without (%) |
19.6 |
17.8 |
9.8 |
6.3 |
7.1 |
16.6 |
5.2 |
8.2 |
| Equivalent AQF |
33 |
36 |
30 |
28 |
28 |
33 |
33 |
27 |
|
| Activity + NSM-1 |
0.65 |
0.39 |
0.46 |
0.54 |
0.44 |
0.54 |
0.28 |
0.40 |
| A.+ NSM-1/Without (%) |
2.7 |
-7.0 |
-0.7 |
0.0 |
-0.2 |
-3.1 |
-2.8 |
-1.5 |
| Equivalent AQF |
26 |
21 |
25 |
25 |
25 |
24 |
24 |
25 |
|
| Activity + NSM-3 |
0.73 |
0.43 |
0.48 |
0.56 |
0.45 |
0.59 |
0.29 |
0.41 |
| A.+ NSM-3/Without (%) |
14.6 |
2.4 |
3.7 |
3.5 |
3.0 |
7.0 |
1.4 |
1.2 |
| Equivalent AQF |
31 |
26 |
27 |
27 |
26 |
28 |
26 |
25 |
|
Table 1: Calculations for several Adaptative Quantization methods
The results are presented in the table 1. The
Activity method reduces consequently the entropy of the coded video. The
NSM however increases the entropy in a proportion function of the amplitude.
The Figure shows the distribution of the Quantization Factor for two pictures
coded with different Adaptive Quantization algorithms at constant entropy.
For each macroblock of the two pictures, a gray color is assigned with
intensity proportional to AQ (White: small AQ, Black:big AQ). The original
files are shown in Figures and .
Figure 3: Visualization of AQ for each macroblock of mobile1 and
popple1 coded with different algorithms at constant entropy
The comparison in terms of picture quality is shown in the table . For
each of the video, different algorithms are classified (1=best).
|
| algorithm |
mobile |
popple |
bicycle |
cheer |
confetti |
flower |
hockey |
tennis |
Average |
|
| without Adaptive Q. |
1 |
3 |
3 |
3 |
1 |
3 |
3 |
3 |
2.5 |
| Activity Model |
3 |
2 |
1 |
1 |
2 |
2 |
2 |
1 |
1.75 |
| NSM-1 |
2 |
4 |
3 |
3 |
1 |
5 |
3 |
5 |
3.25 |
| NSM-2 |
5 |
6 |
6 |
3 |
1 |
6 |
3 |
6 |
4.5 |
| NSM-3 |
6 |
7 |
6 |
6 |
1 |
7 |
3 |
7 |
5.35 |
| Activity + NSM-1 |
4 |
1 |
1 |
1 |
2 |
1 |
1 |
2 |
1.6 |
| Activity + NSM-3 |
7 |
5 |
3 |
6 |
2 |
4 |
3 |
3 |
4.1 |
Table 2: Classification of the different methods for seven video.
The table 2 shows that:
-
the NSM is not efficient if applied alone.
-
the best adaptive quantization model is a combination of the Activity model
and NSM-1. But the difference with the Activity model alone is not big.
4.3 Explanation of the
results
The results are not as good as expected after the study presented in
[]. Of course, the combination with the activity model improves a little
bit the picture quality, but the cost in calculation is too big compared
to the real improvement. The difference with expectations may have many
sources: The noise sensitivity model could be not adapted in the case of
a compression algorithm; the activity factor and NSM correction factor
may not be perfectly orthogonal. The model can't anyway be used as it is,
and big changes should be envisaged to make it useful.
Indeed, the Perceptual Noise Sensibility Measurement has been elaborated
by adding noise to video with very low activity, essentially flat regions.
But in a compression algorithm, this regions have low entropy and no bitrate
gain can be expected. Therefore, it has to be efficient also for middle
and high activity regions, and that has not been proved. Likewise, the
compression algorithm behaves as a low pass filter. Therefore the sensibility
to high frequency noise might not be the same as the sensitivity to block
effect or other undesirable effects found in decoded video.
5 Possible improvements for
the previous Adaptative Quantization method
5.1 Separating the quantization
of Y, Cb, and Cr blocks
The MPEG-2 standard allows only the transmission of a single quantization
factor per macroblock. Because of that, the present quantization method
is focalized principaly on the four luminance blocks. In the Activity Model,
for example, the correction factor only depends on the luminance. In the
proposed NSM, a tentative for taking the chrominance values into account
has been done, but still no real separation has occurred. In this section
two different quantization methods are proposed allowing a more concrete
separation.
-
For each macroblock, three quantization factors are calculated instead
of one: AQY, AQCb and AQCr. AQmin
will be the minimum of them and the one to be transmitted. By now, the
equation (4) is used. To make it more clear, let's
simplify it to:
| ac_quant(i,j) = (int) |
æ
ç
è |
|
ac(i,j)
2AQ |
|
ö
÷
ø |
, |
|
(14) |
where (int)(x) is integral value of x. The idea is to calculated instead:
| ac_quant(i,j) = (int) |
æ
ç
è |
|
AQx
AQmin |
(int) |
æ
ç
è |
|
ac(i,j)
AQx |
|
ö
÷
ø |
|
ö
÷
ø |
, |
|
(15) |
where x = Y if i = 1,2,3 or 4, x = Cb if i = 5 or 6, x = Cr if i = 7 or
8. In this case, only AQmin is transmitted but still the blocks
concerning Y, Cb and Cr are coded with a specific precision.
-
The second method consists in varying the dead zone (DZ) in the Quantization
process. It can indeed be changed for each subblock of a given macroblock.
Depending on the color coordinates for example, three different DZ could
be set for the Y, Cb and Cr blocks. The Figure () illustrates the method.
Figure 6: Dead Zone as a quantization factor
5.2 Further possible research
Even if the results presented in the previous section are not as good as
expected, a color dependent quantization factor still remains a possible
way to improve the picture quality: the luminance is important but it shouldn't
be the only parameter like in TM5. The chrominance coordinates should also
be taken into account.
Here are listed some possible research directions:
-
By now, the NSM and the Activity model have been considerate as independent.
Therefore, when used together, the correction factors have just been multiplied.
This combination might be too simple, especially when the activity is very
low or very high. In the first case indeed, the precision should be maximum
because a low entropy. In the second case, the NSM has no real meaning
as explained before. A possible improvement, could be therefore to find
the activity range in which the NSM is valid and to use it only within
this limits.
-
If the NSM is proved to be unadapted to compression algorithms, a limited
model could be used instead, giving a sensitivity depending, for example,
only on the luminance.
-
The possible separation between Y, Cb and Cr subblocks for quantization,
can also be tested: concerning the Activity Model, three N_actj would indeed
be calculated for the three color coordinates. Apropos the NSM, three color
correction factors could also be calculated by normalizing directly RNxY,Cb
or Cr,j.
-
Some human perception based thresholds could also be calculated deciding
the length of the Dead Zone for Y, Cb and Cr.
-
A Perceptual Noise Sensitivity model has been elaborated. The same could
be done for some effects observed on a decoded video: Block effect... It
could depend on the color, like for the NSM, but also on the activity or
the presence of bounds.
6 Conclusion
In this report, the results of several algorithms of Adaptive Quantization
are exposed. In a first part, the Activity Model of the TM5 and a new color
dependent model are described. This new model is based on a Perceptual
Noise Sensitivity Measure introduced in the report. In a second part, the
different algorithms are tested. The new model is not efficient if used
alone, but it improves slightly the picture quality if used together with
the Activity Model. The improvement is unfortunately very small. In the
last part of the report some new possible adaptive quantization algorithms
are suggested. They are based on a separation, in the quantization process,
of the Y, Cb and Cr subblocks.
References
-
[]
-
Herve Galleron, ``Color Dependancy of Perceptual Noise Sensitivity''
Internal Report (March 1998).
File translated from TEX by TTH,
version 1.58.